I recently had the good fortune of learning Marion Walter’s theorem from Marion Walter herself:
Marion Walter’s Theorem: In a triangle, draw line segments from each vertex to the trisection points on the opposite side. The six drawn line segments will form the edges of a central hexagon. The ratio of the area of the hexagon to that of the whole triangle is 1/10.
An efficient way to prove Marion Walter’s theorem is to use mass points.
In this post, I’ll give details because the proof is a model example of the mass points technique. If you’re having difficulty learning the technique, I hope this post will help it all come together for you. As always, try to use mass points to prove the theorem yourself, and, only after you have tried, read on. If you’ve never heard of mass points before, please google it or check out Volume 7, Number 3 of the Girls’ Angle Bulletin (in particular, please read pages 12-14 and pages 19-22 of that issue) before reading further, because here, we’re going to show how the mass point technique is used to prove Marion Walter’s theorem and only sketch how the method itself works.
Spoiler Alert! Proof Below!
It all begins with Archimedes’ Law of the Lever, which we will apply over and over.
Two point masses connected by a massless rod will balance at their center of mass. Archimedes tells us that the distances of each mass from the center of mass satisfy the equation .
The center of mass will lie along the line segment connecting the two masses and sit nearer the heavier one. If the masses are equal, then the center of mass will be exactly halfway between. If one mass is twice the other, then the center of mass will be 2/3 of the way from the lighter to the heavier. (In general, the center of mass is the weighted average of the positions of each object weighted by the mass of that object.)
For a proof of this “piecemeal” way to compute the center of mass and for more information about the center of mass and other applications, see, for instance, Section 19.1 of the Feynman Lectures on Physics, Volume 1, or checkout Volume 7, Number 3 of the Girls’ Angle Bulletin, particularly page 20.
In addition to the Law of the Lever, a beautiful property of the center of mass that we will use repeatedly is that the center of mass can be computed piecemeal. That is, we can split the objects into different sets, compute the center of mass of the objects in each set separately and pretend that each set is replaced by a single point mass equal to the total mass of the objects in that set and located at that set’s center of mass. Then we can compute the center of mass of these pretend point masses to learn the location of the center of mass of the original collection of objects.
For point masses, this “piecemeal” fact enables us to find the center of mass of any number of point masses with repeated application of Archimedes’ Law of the Lever. All we have to do is compute 2 masses at a time, as illustrated in the following figures.

To find their center of mass, we can proceed 2 masses at a time. If we start with the first 2 masses, their center of mass will be somewhere along the line segment connecting them.

We pretend there’s a point mass at the center of mass of the first 2 masses with mass equal to their sum. The exact location of the center of mass is determined using Archimedes’ Law of the Lever.

To find the center of mass of the original 3 point masses (indicated by the red dot), we find the center of mass of the imagined green point mass that we computed in the previous step and the 3rd mass. The exact location of the red dot can be determined again using Archimedes’ Law of the Lever.
Proof of Marion Walter’s Theorem
Here’s a figure illustrating Marion Walter’s theorem with the 3 medians of the triangle added in.
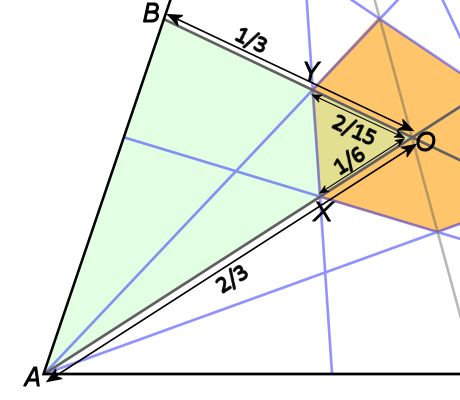
We’ll focus on the green triangle and compute how much of the tip of that triangle is inside the orange hexagon:
Let be the measure of
.
The area of triangle XOY is .
The area of triangle AOB is .
Therefore, the ratio of the area of triangle XOY to the area of triangle AOB is:
.
To compute these two ratios of lengths, we will use the technique of mass points to compute each length as a fraction of the length of the cevian that it lies on.
Back to the larger figure:
Let’s start with the indicated lengths (which correspond to OY and OB in the labeling of the prior diagram). We’ll use mass points to figure out their lengths as a fraction of the median they’re both on. Let’s start with the longer length.
If we knew what masses to place at the endpoints of the median so that their center of mass sat at the intersection of the medians, then we could use Archimedes’ Law of the Lever to compute the ratio of the lengths that the median is split into. But the problem is, we don’t know that ratio. That’s essentially the ratio we’re trying to find.
What we do know is the ratios of key lengths along the sides of the triangle, because the whole problem is set up by trisecting the sides. This suggests using 3 masses, one at each vertex, as shown below:
Can we figure out how to assign masses to the 3 vertices so that the center of mass of all 3 masses will be where the medians intersect?
Notice that if the two leftmost masses are equal, then, by Archimedes’ Law of the Lever, their center of mass will be at one end of the red median, since the median bisects the side. The importance of assigning the 2 leftmost masses so that their center of mass is at one end of the red median is that it guarantees that the center of mass of all 3 masses will lie on the red median (because of the “piecemeal” property for computing the center of mass).
When the unknown mass (indicated by “?”) is zero, the center of mass of all 3 masses will be midway between the two leftmost masses. As the unknown mass increases, the center of mass of all 3 masses will move along the red median toward the unknown mass. What must the unknown mass be so that the center of mass of all 3 masses will be right where the medians intersect?
We know we can compute the center of mass of the 3 masses piecemeal, and we used this fact to see that by making the 2 leftmost masses equal, the center of mass of all 3 masses will be somewhere on the red median. And now comes a key idea: if we cleverly arrange it so that the center of mass of the 2 lower masses is exactly halfway between them, then the center of mass of all 3 masses will also lie along a second median, and, therefore, it will be at the intersection of both medians!
In other words, to make the center of mass of all 3 masses be at the intersection of the medians, we now only have to concentrate on making the center of mass of the lower 2 masses be at their midpoint. Using Archimedes’ Law of the Lever, we know this happens when the unknown mass is also m.
Thus, the center of mass of 3 equal masses placed at the vertices of a triangle is located at the intersection of the triangle’s medians.
Now, we can compute the ratio of the lengths that the red median is split into by the other medians. We go back to computing the center of mass piecemeal by first computing the center of mass of the 2 leftmost masses and imagining a single point mass of mass 2m placed there. We’ve purposefully assigned the masses so that the center of mass of this 2m-mass and the m-mass in the lower right corner will be at the intersection of the medians, hence the ratio of the lengths that the red median is split into, by Archimedes’ Law of the Lever, must be 1 : 2. We deduce that the length we are looking for (indicated by the double-headed arrow) is 1/3 the length of the red median.
Now let’s turn our attention to the other length:
This time, we try to assign masses to the vertices so that their center of mass will be where the red and orange cevians intersect in the figure below.
Since the red cevian is a median, we know to place equal masses at the 2 leftmost vertices, just as before. This time, however, we want to assign a mass to the lower right vertex in such a way that the center of mass of the 2 lower masses will be at the foot of the orange cevian, which is 1/3 of the way from left to right. Using Archimedes’ Law of the Lever, we compute that the lower right mass must be m/2.
We now compute the center of mass piecemeal, starting with the 2 leftmost masses. Their center of mass is at the foot of the red median (by design), so we imagine a point mass of mass 2m placed there. The red median is split into two pieces by the orange cevian. Archimedes’ Law of the Lever tells us that the ratio of the lengths of these two pieces is equal to the ratio m/2 to 2m, which is 1/4. Hence, the center of mass of these 3 point masses is 1/5 of the way along the red median, measured from its foot.
Therefore, the distance we’re interested in (indicated by the double-headed arrow in the figure above) is 1/3 – 1/5 = 2/15 of the length of the red median.
Next, we turn our attention to the other 2 important lengths indicated below:
What fraction of the purple median are they?
The longer length stretches from the vertex to the intersection of the medians, and we already know how to balance the triangle there. That’s achieved with equal point masses at each vertex and we conclude that the longer length is 2/3 of the length of the purple median.
For the shorter length, we try to assign point masses to the vertices so that their center of mass is where the purple median and orange cevian intersect. The figure above shows what the masses need to be to achieve that. Computing this center of mass location piecemeal, starting with the 2 rightmost masses and then applying Archimedes’ Law of the Lever, we find that the orange cevian actually bisects the purple median! Hence, the shorter length is 2/3 – 1/2 = 1/6 of the length of the purple median.
Putting it all together, we find that:
.
(Note that the numbers are fractions of lengths, not absolute lengths. That is OX is not 1/6 nor is OA equal to 2/3, but since we are taking ratios, OX/OA is equal to (1/6)/(2/3).)
To find the fraction of the triangle’s area that the hexagon occupies, we note that the tips of the 6 green triangular sections that dip into the hexagon are all 1/10 of their respective green triangles. That’s because the computations for each green triangle will look just like the computation we just went through by symmetry.
Therefore, the area of the hexagon, which consists of the 6 tips of the green triangles, is exactly 1/10 the area of the whole, and the theorem is proven.
To show how efficient this technique is, I’ve scanned in my actual scratch work. When you’ve gotten the hang of the mass point technique, you can compute the necessary masses “as you go.”
One set of mass assignments is uncircled and the other set is circled. After the fact, I tried to indicate which parts of the computation correspond to which line segments in the figure.
For more practice with mass points, there is a Summer Fun problem set devoted to the technique by Johnny Tang in the latest issue of the Girls’ Angle Bulletin (Volume 7, Number 5). Also, check out these lecture notes by Tom Rike for a talk he gave at the Berkeley Math Circle. At MathWorld, there’s a slightly different approach to proving Marion Walter’s theorem that also essentially uses mass points. There are many other proofs that use different techniques, such as the one outlined at the end of this handout by James King.
















Pingback: Celebrating Marion Walter – and other unsung female mathematicians | YubaNet
Pingback: Unsung Female Mathematicians: Celebrating Marion Walter
Pingback: Celebrating Marion Walter – and other unsung female mathematicians - DJG Blogger